[제 1편] 딥러닝의 시작과 인공신경망
2019년 05월 25일 | by Admin
딥러닝 연재 시리즈
제 1편. 딥러닝의 시작과 인공신경망
제 2편. CNN 소개 및 CNN 기반의 다양한 알고리즘과 활용 사례
번외편. 딥러닝 개발환경 구축하기
제 3편. 자연어 처리 이해하기
제 4편. RNN, LSTM 소개 및 RNN, LSTM 기반의 다양한 알고리즘과 활용 사례
1. 딥러닝의 시작 (들어가기)1.1 AI, 머신러닝, 그리고 딥러닝의 구분1.2 인간의 신경망과 인공신경망1.3 인공신경망의 용어1.4 실제 서비스에 사용되는 다양한 신경망 소개 1.5 소결 (제 1장을 마치며) 2. 인공신경망 깊게 이해하기 2.1 단일 퍼셉트론에서 일어나는 일 2.2 단일 퍼셉트론을 활용한 부도여부 예측2.3 단일 퍼셉트론의 한계2.4 다중 퍼셉트론의 등장 (MLP) 2.5 2장 소결3. 인공신경망 구현해보기
1. 딥러닝의 시작 (들어가기)
안녕하세요? 제가 다룰 내용은 AI에 대한 내용 중, 딥러닝(Deep learning)에 대한 내용을 다뤄볼까 합니다. 많은 분들이 딥러닝과 인공지능에 대해 한번쯤은 다 들어보셨을 거라고 생각합니다. 2016년 이세돌과 알파고의 대전 이후 인공지능에 대한 관심이 증대하고, 지금은 딥러닝 기반 서비스들이 많이 등장하고 있습니다.
하지만 막상 공부하려고 하면 AI가 무엇이고 딥러닝은 또 무엇인지? 또 딥러닝을 공부하다 보면 머신러닝도 알아야 할 것 같고 그렇습니다. 딥러닝에 대해 설명하고 있는 책자나 블로그를 읽다 보면 "딥러닝은 머신러닝 계열인데…인공신경망 기반의 어쩌고…" 라는 문장을 보기도 합니다. 그러면 또 도대체 머신러닝..이 무엇인지? "learning" 한다고 하는데 컴퓨터가 무엇을 배우는 것인지? 너무나 추상적이셨을 겁니다.
그래서 저의 목표는 다음과 같습니다. 1편에서는 딥러닝이 갖는 추상적인 개념을 명확하게 구분하고, 더 나아가 딥러닝의 기본이라고 할 수 있는 인공신경망에 대해 알아 보도록 하겠습니다. 이후 2편에서는 이미지 인식을 위한 CNN 모형과 해당 모형을 활용한 사례, 그리고 CNN 모형을 구현하도록 하겠습니다. 2편 이후에는 번외편을 통해 개발 환경 구축방법을 설명드리며, Python Jupyter 환경구성 또는 Cloud 기반의 딥러닝 개발 환경 구축에 대해 설명하겠습니다. 제 3편에서는 자연어 처리에 대한 설명과 함께, 제 4편에서는 자연어 및 연속된 데이터 분석에 특화된 LSTM 모형 설명과 실제 구현, 그리고 응용사례를 살펴보겠습니다.
1.1 AI, 머신러닝, 그리고 딥러닝의 구분
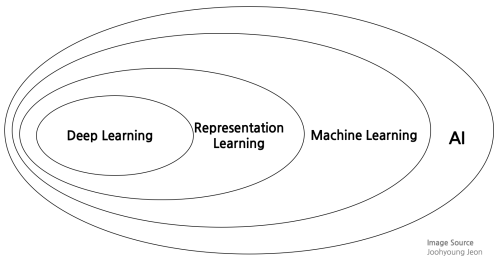
[그림 1]은 AI라는 큰 개념이 포함하고 있는 하위 3개의 세부속성으로 분류한 다이어그램입니다.
(1) AI
요즘 말하는 AI(Artificial Intelligence)라는 개념은 오래전부터 존재 하였고, 과학자들의 무수한 연구대상 이었습니다. 그럼 AI의 명확한 정의는 무엇일까요? 단순히 기계가 사람처럼 움직이면 AI라고 할 수 있을까요? AI에 대한 정의 하나를 소개하도록 하겠습니다. 영화 이미테이션 게임의 주인공인 '앨런 튜링' 한번 은 들어 보셨을 겁니다. 그는 인공지능의 아버지라고 불리는데, 앨런 튜링이 그렇게 불릴 수 있었던 이유는 '튜링 테스트'라는 인공지능 시스템을 테스트 하는 방법을 처음 제시했기 때문이죠.
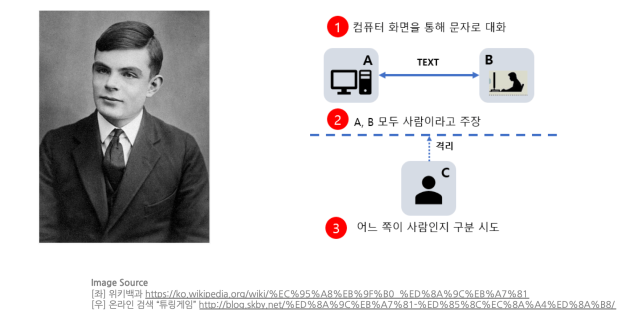
튜링 테스트는 기계(A)와 사람(B)의 대화를 제3자(C)가 듣고선, 제3자(C)가 기계(A)와 사람(B) 중 누가 기계인지 분별하기 어려운 경우, 해당 기계(A)는 튜링 테스트를 통과하게 됩니다. "컴퓨터로부터의 반응을 인간과 구별할 수 없다면, 컴퓨터는 생각 할 수 있는 것" 이라고 말이죠. 이러한 튜링 테스트의 관점에서 AI란 기계에게 "지식" 과 "경험"을 가르쳐주는 것이고 이를 통해 사람 처럼 행동하는 모든 유형의 기계를 의미한다고 할 수 있습니다. 매우 넓~은 범위의 개념이죠. 그리고 이를 구현하기 위한 다양한 알고리즘이 존재합니다. 그렇다면, 기계가 배워야 하는 지식과 경험이 무엇인지, 그리고 또 어떻게 이를 가르쳐 줘야 진정한 AI가 태어날 수 있는지 한번 그 여정을 떠나보도록 하겠습니다.

참고로 튜링은 2차 세계대전 당시 독일의 암호체계였던 에니그마를 해독할 수 있는 기계를 개발한 과학자이기도 하고, 현대 컴퓨터 체계를 수립한 존 폰 노이만의 제자이기도 했습니다. 존 폰 노이만이 그의 지도교수 였었죠. 하지만, 튜링은 성 정체성의 혼란으로 인해… 화학적 거세를 당했고, 자기 스스로 독이 든 사과를 한입 베어먹고 자살합니다. (그리고 마법사로 부활했죠..)
(2) Machine Learning
위에서 살펴본 바, AI 시스템으로 거듭나기 위해서는 지식과 경험을 가르쳐줘야 한다고 했습니다. 과연, 어떻게 할 수 있을까요? 왠지 그것에 대한 해답은 Machine Learning에 있을 것 같지 않나요?
머신러닝(Machine Learning)의 학문적 정의는 Tom Mitchell이 그의 저서 Machine Learning[1997] 에서 사용한 "컴퓨터 프로그램이 특정 업무(T)를 수행할 때 성능(P)만큼 개선되는 경험(E)를 보이면 컴퓨터 프로그램은 해당 업무(T)와 성능(P)에 대해 경험(E)를 학습했다고 할 수 있다." 가 있습니다. 이에 대한 간단한 예를 들어보겠습니다.
컴퓨터에게 사과와 딸기 이미지를 인식하고 분류하는 업무를 부여한다고 했을 때, 머신러닝의 관점에서는
T : 사과/딸기 이미지를 인식하고 분류하는 것 P : 사과/딸기 이미지를 정확하게 구분한 확률 E : 사과/딸기 이미지를 표현한 Matrix 와 label 값(사과 : 1/ 딸기 : 0)을 가지고 있는 데이터셋 입니다.
컴퓨터에게 E를 계속 보게 하여, T라는 업무를 수행함에 있어 과거의 P가 50%였던 것을 80%까지 끌어올렸다면, 미첼이 말했던 머신러닝 관점에서는 30%의 성능향상이 있었기에 해당 프로그램은 T업무와 이를 잘 분류한 80%(P)에 대해 경험(E)를 학습했다는 것 입니다. 이것이 머신러닝 입니다.
소위 말하는 "데이터를 학습한다" 라고 말하는 그 "데이터"의 중요성이 바로 여기에서 나온 것이고, 실제로 그렇습니다. 머신러닝이든 딥러닝이든 학습하는 데이터가 매우 중요합니다. 그래서 Garbage in Garbage out(GIGO) 이라는 용어도 있지요. AI가 되기 위해 "경험" 을 학습해야 했는데, 그것을 바로 이 머신러닝이 할 수 있는 것 입니다. 이제 우리는 두 번째 영역에 들어왔네요 !!
(3) Representation learning
Representation은 그 뜻 자체로 '표현', '대표' 등의 뜻이 있습니다. 무엇인가를 대표한다는 것이죠. 잠시 (2)머신러닝의 예제였던 사과와 딸기를 인식하고 분류하는 문제로 넘어가겠습니다. 우리는 T라는 과업에서 P의 향상을 위해 E를 학습한다고 했습니다. 여기서 E는 데이터셋 인데요, 머신러닝에서 말하는 represenation learning 이란 훈련하는 알고리즘이 학습 과정에서 데이터(E)의 중요한 특징을 스스로 파악한다는 것 입니다.

우리는 어렸을 적 낱말카드를 보며 사물을 인식하는 T를 해 왔습니다. 사과, 딸기가 그려진 그림을 보며 맞추는 행동이었죠. 둘다 색깔은 유사합니다. 하지만, 위에 꼭지가 있거나 역삼각형의 모습을 보이고 검정색 점이 겉면에 송송 붙어있으면 "딸기" 라고 인지했고, 전반적으로 둥글고 크고 빨간색 광택이 나는 것은 "사과"라고 인식 했습니다.

이처럼, Representation learning은 데이터 에서 중요한 특징(Feature)을 알고리즘이 감지하는 것을 의미합니다. 특정 부분을 감지한다는 것은, 해당 데이터와 연결된 신경망 가중치를 더욱 크게 한다는 것 인데요, 이는 2장에서 조금 더 자세하게 설명하겠습니다.
아무쪼록 AI > Machine learning > Representation learning 까지 들어왔습니다. 그 다음 등장하는 Deep learning이 바로 Representation learning을 알고리즘이 "알아서" 잘 하는데 최적화 된 녀석들 입니다. 특히, 추후 다룰 알고리즘인 CNN(convoulation neural networks)은 이미지 데이터에서 중요 특징을 감지하는데 아주 선수입니다.
(4) Deep learning
이제야 딥러닝의 영역까지 왔습니다. 앞에서 나온 (1),(2),(3)의 정의를 쭉 정리해보자면 다음과 같습니다.
"무엇이 AI시스템이냐?"
라는 질문에 대답하기 위해 여러 관점 중 앨런 튜링의 '튜링 테스트'를 인용하면, AI란 "제 3자가, 보이지 않는 두 화자의 대화에서 어떤 화자가 컴퓨터인지 구분할 수 없다면, 그 시스템은 AI시스템이다." 라는 것이 있었습니다. 그러면,
"어떻게 AI 시스템을 만들 것이냐?"
라는 질문에는 기계에게 "지식"과 "경험"을 가르쳐야 한다고 했습니다. 이를 위해 머신러닝 계열의 알고리즘은 데이터를 통해 경험을 학습시켜 줍니다. 또한, 수 많은 경험(데이터)에서 알아서 핵심적인 경험을 추출하고 학습하는 알고리즘을 Representation learning) 이라고 합니다.
논의를 정리함과 동시에 [그림 1]을 참고하면, 딥러닝이라는 기술은 결국 AI라는 광범위한 분야 중, 머신러닝 이면서 동시에 데이터에서 핵심을 잘 선별해내는 기술이라고 할 수 있습니다. 그리고 이러한 분야에 매우 유능한 알고리즘이 하나 등장합니다. 바로 인공신경망(Artificial Neural Networks) 이죠.
인공신경망 = AI?
인공신경망은 인간의 신경체계를 모사한 알고리즘 이기도 하기 때문에, 이름 부터가 인공신경망(Artificial Neural Networks) 입니다. 이러한 이유로, 혹 누군가는 "인공신경망 = AI" 라고 생각하시는 분들도 있는데, "인공신경망 = AI"는 결코 아닙니다. AI라는 거대한 집합(Set)이 있으면 (그것을 구현하기 위한 하나의 기술) 집합의 한 원소(Element)로 인공신경망이 존재하는 것 입니다. 이와 유사하게도, 유전 알고리즘(genetic algorithms)이라고 1960년대에 나온 알고리즘이 있는데요, 이것은 John Holland가 찰스 다윈의 "진화론"에 영감을 받아 제안한 알고리즘 입니다. 생물의 진화체계를 모사했죠. 그러면, 이것 역시 AI 아닌가? 라는 생각이 드실 겁니다. 실제로 인공신경망이 쇠퇴기를 맞았던 90년대 까지 유전알고리즘이 대세였습니다. 당시 나온 인공지능(Artificial Intelligence)을 기술적으로 다루고 있는 책들을 보면, 하나같이 유전알고리즘을 다루고 있었지요. 하지만 "genetic algorithm = AI"는 아닙니다. AI라는 개념은 더욱 넓고 방대한 영역이기 때문에 그것이 정확하게 "무엇이다." 라고 구체화 할 수 없습니다. 다만, AI 시스템을 구현하기 위한 여러가지 기술들이 있는 것이고 그 중 하나가 인공신경망 입니다.
따라서, 저희가 다룰 내용은 AI라는 거대한 시스템으로 다가가기 위해 필요한 도구 중 하나인 "인공신경망"을 다뤄볼까 합니다. 그렇다면, 이렇게까지 길게 글을 써가면서 "인공신경망"을 말씀 드렸던 이유는 무엇이며? 또 많은 기술자들은 이것에 열광하는 것 일까요?? 궁금하지 않으신가요!?
1.2 인간의 신경망과 인공신경망

(1) 인간의 신경망
사람의 뇌 속에는 다수의 뉴런들이 네트워크 형태로 구성되어 있습니다. 서로 연결되어 있어 뉴런 하나가 다른 뉴런에게 신호를 전달하는 구조입니다. [그림 6] 에서 상단은 실제 인간의 신경망을 나타낸 것이며, 하단은 인공신경망의 구조를 나타낸 것 입니다.
우리는 눈(시각), 피부(촉각), 귀(청각), 혀(미각), 코(후각)의 감각기관으로 부터 자극을 받습니다. 이때 자극은 가지돌기(또는 수상돌기, dendrite)를 통해 받아들여 집니다. 가지돌기에서 받아들여진 자극은 신경세포체(뉴런의 본체, Neuron cell body)로 전달됩니다. 그럼 뉴런은 여러 가지돌기로 부터 전달된 입력신호를 합하여 반응 여부(activate)를 판단하고, 신호를 보내야 하면 축삭돌기(또는 축돌기, axon) 끝의 시냅스를 이용해 다음 뉴런에게 신호를 전달합니다.
하지만 뉴런은 모든 신호를 전부 다음 뉴런에게 전달하는 것은 아닙니다. 뉴런은 여러 뉴런들에게 받은 신호들을 다시 합하여 일정 임계값(threshold)을 넘어가는 것들만 다음 뉴런에게 전달합니다. 만약, 뉴런이 모든 입력신호를 다 전달하게 된다면 그 사람은 사소한 신호에도 신경계가 전부 흥분하는 것을 뜻하며 이는 정서 불안정 상태가 되겠지요.
(2) 인공신경망
그렇다면 인공신경망은 어떤 형태일까요? [그림 6] 하단은 인공신경망 모습입니다. 여기서 그림 맨 좌측 는 입력신호를 말합니다. 인간의 신경계로 따지면, 감각기관을 통해 받아들여진 일종의 감각입니다. 데이터들은 화살표를 통과하여 다음 원으로 전달됩니다.
데이터를 받아들이는 부분은 일종의 가지돌기 역할을 수행합니다. 그런 다음 신경세포체에게 전달됩니다. 그림에서 신경세포체는 원을 말합니다. 그래서 많은 인공신경망 교과서에는 저 부분을 '뉴런'과 비슷하다고 말합니다. (어떤 곳에서는 그냥 신경세포체 라고도 합니다. 핵심은 저 동그라미의 원이 인간 뉴런과 유사한 역할을 수행한다는 것 입니다. )
그림에서는 첫 번째 층은 3개의 뉴런으로 구성되어 있습니다. 각각의 뉴런은 부터 까지의 데이터들을 다 받아들이고, 신경의 합을 구합니다. 마찬가지로 2번째, 3번째 뉴런도 개의 입력 데이터들을 다 받아들입니다. 그런 다음, 3개의 뉴런들은 입력받은 데이터들이 임계값을 넘어가는 지 여부를 결정합니다.
(사람의 뉴런과 달리, 인공신경망의 뉴런은 그 자체가 임계값을 설정해놓고 있지 않습니다. 해당 부분의 논의는 제 2.1장 단일 퍼셉트론에서 일어나는 일에서 상세하게 설명하겠습니다.)
논의를 간편하게 하기 위해, 3개 뉴런 중 가운데 뉴런의 신호가 임계값을 넘는다고 가정하겠습니다. (빨간색 원) 그러면, 해당 부분의 신호가 다음 뉴런에게 전달됩니다. 그리고, 전달받은 뉴런은 최종 마지막 1개 뉴런에게 신호를 전달하며, 마지막 뉴런은 해당 신호에 대해 반응할지 여부(1/0)를 결정합니다.
이러한 정보를 토대로 우리가 알아가야 할 인공신경망에 대한 용어를 한번 정리해보도록 하겠습니다.
1.3 인공신경망의 용어
인간 신경계의 기능과 부위에 대해 알아 보았습니다. 가지돌기(또는 수상돌기), 신경세포체(뉴런에 존재하는 핵), 신경의 합을 구해 임계값을 넘는지 여부, 축삭돌기(신호의 전달부분)가 있었습니다. 그렇다면, 이러한 기능을 수행하는 부위를 인공신경망에서는 어떻게 구현하고 있으며 무엇이라 부르는지 한번 살펴보겠습니다.

[그림 7]은 다층 인공신경망 입니다. 다층과 단층을 구분하는 개념은 본 용어정리 이후에 말씀드리도록 하겠습니다. 인공신경망은 다음과 같이 3가지 층(Layer)으로 나누는 것을 기본으로 하고 있습니다.
- Input Layer (입력층) : 데이터가 입력되는 계층 (가지돌기의 역할)
- Hidden Layer (은닉층) : 데이터가 전달되는 계층 (뉴런-시냅스-축삭돌기-뉴런 등 신호의 전달 계층)
- Output Layer (출력층) : 데이터가 출력되는 계층 (운동기관을 통해 반응여부를 결정하는 기능)
- Units : 데이터를 받아들여 다음 계층으로 전달할지 판단 (신경망 뉴런의 역할)
- Weights : 전/후 Units를 잇는 화살표, 각 Units의 연결강도를 결정하는 가중치 (시냅스 틈을 타고 전달되는 신경 전달 물질의 강도, 특정 감각에 대하여 민감한지 둔감한지 여부)
- Activation (Function) : Units에서 다음 신호로 보낼지 판별하는 함수 (뉴런에서 계산된 값이 임계치를 넘는지 여부와 이를 토대로 다음 신호 전달여부를 활성화 할 것인지 판단)
이러한 기준에서 [그림 7]에서 표현된 인공신경망은 입력층 1개, 은닉층 2개, 출력층 1개. 총 4개의 층(layer)로 구성된 인공신경망이라고 할 수 있겠죠? 하지만! 주의해야 할 점은 입력층은 인공신경망 전체 구성을 말할 때 빼줍니다. 따라서, [그림 7]의 인공신경망은 3개의 층으로 구성된 신경망 이라고 합니다. 층의 수를 셀 때 입력층을 제외함을 유의하세요.
- 다층 인공신경망 (Multi-Layer Perceptron)
이를 토대로, [그림 7]과 같은 구조의 인공신경망을 말할때 "4차원의 입력 데이터를 받는 3개 층으로 구성된 다층 인공신경망" 이라고 합니다. 이를 MLP(Multi-Layer Perceptron)라고 부릅니다. 새로운 용어가 등장했습니다. 바로 퍼셉트론(Perceptron) 인데요.
퍼셉트론은 1957년 프랑크 로젠블라트(Frank Rosenblatt)에 의해 고안된 인공신경망으로, 위에서 언급한 인간 신경을 가장 유사하게 모사한 신경망을 말합니다. 가중치와 입력값의 합이 활성함수에 들어가 임계치를 결정하고, 결정된 임계치가 다음 뉴런으로 전달되는 형태의 신경망을 퍼셉트론 이라고 합니다.
여기서 더 나아가, "퍼셉트론" 이라는 신경망이 존재하는데 그렇다면 다른 유형의 신경망도 존재합니까? 라는 질문이 있을 수 있습니다. (디셉티콘, 옵티머스는 없습니다)
정답은 물론입니다. 1950년대 후반 신경망 발달 과정에서 과학자들은 다양한 형태의 인공신경망을 제안했습니다. 퍼셉트론은 여러 신경망 중 하나의 신경망 입니다. 다른 유형의 신경망은 추후 말씀드리도록 하겠습니다.
심층신경망(DNN, Deep Neural Networks)은 바로 위와 같은 구조의 신경망에서 은닉층의 개수가 2개 이상인 것을 말합니다. 물론 5개 이상이어야 심층신경망이다. 라고 하는 분들도 있습니다. 중요한 것은,층이 2개냐 5개냐가 아니라, 은닉층을 여러개 쌓아 올린 것을 바로 심층신경망 이라고 부르는 것이며 지금 이 부분부터는 여러분들이 바로 딥러닝(Deep Learning)을 배웠다! 라는 것 입니다.
(간혹 딥러닝 책을 읽다 보면 등장하는 Deep 0000 이라는 이름은 이러한 신경망을 엄청 깊게 만든 것 입니다.)

[그림 8]의 신경망을 4개의 층으로 구성된 심층신경망 이라고 합니다.
좀 더 자세하게 말씀드리면, 입력 받은 데이터 차원이 8이며(), 각 Hidden Layer의 Units의 수가 9개이고 최종 출력층의 output units은 4개인 심층신경망 이라고 부를 수 있습니다. (4개의 값으로 출력됩니다)
여기에서 1장의 내용을 멈추고자 합니다. 단일 퍼셉트론이 갖는 단점 및 Activation 함수의 선정 등 인공신경망에 대하여 더 깊게 들어가는 내용은 "제 2장 인공신경망 깊게 이해하기" 에서 다루도록 하겠습니다.
1.4 실제 서비스에 사용되는 다양한 신경망 소개
이제, 여러분은 딥러닝 중 기본이 되는 DNN에 대해 한번 살펴 보셨습니다. 본 글을 읽어주시는 독자께서 전부 엔지니어는 아니기 때문에 여기에서 멈춰야 할 필요가 있을 것 같습니다. 따라서, 현재 딥러닝 기술을 통해 어떤 서비스들이 이뤄지고 있는지 한 장의 표로 정리하고 1장을 마무리하고자 합니다. 만약, 이 글을 읽어주시는 독자께서 딥러닝 기반 기술을 더욱 자세히 알고 싶다 하시면, 제 2장부터 쭉 읽어 주시면 감사하겠습니다. (저 또한 매우 좋습니다 ^^)
| 서비스 유형 | 딥러닝 모형 (주로 활용되는 알고리즘) |
|---|---|
| 이미지 판별, 객체인식, 얼굴인식 | CNN (VGG, ResNet, GoogleNet, Inception, R-CNN, YOLO) |
| 챗봇, 음성스피커, 기계번역 | RNN, LSTM, Seq2Seq, Attention, BERT |
| 이미지 합성, 이미지 생성, 화자판별 | Neural Style Transfer, GAN, DCGAN |
| 자율주행 | CNN 계열을 통한 동적/정적 객체 인식, 강화학습 통한 움직임 정의 |
(1) 이미지 인식
이미지 처리와 관련된 대부분의 알고리즘은 CNN(Convolution Neural Networks)을 기반으로 하고 있습니다. CNN의 경우 본 저널의 제 2편. CNN 소개 및 CNN 기반의 다양한 알고리즘과 활용 사례에서 깊게 다룰 예정입니다. 간략하게 말씀드리면, DNN의 경우 망이 깊어질 수록 weights가 많아지며 이는 Computation Power에 큰 영향을 미칩니다. 만약, 여러분 휴대전를 통해 찍은 사진에서 물체를 인식하는 문제를 DNN을 통해 해결해야 한다고 가정하겠습니다. 입력되는 사진의 화소가 2,048 px * 2,048 px 이라면, 입력층의 유닛 수는 2,048 * 2,048 = 4,194,304개 입니다. 그리고, 바로 다음에 연결된 첫 번째 히든레이어 유닛의 수가 정확하게 1,000개라면 입력층과 바로 다음 히든레이어가 연결될 때 필요한 weights의 개수는 4,194,304,000 + 1,000(bias)로 대략 41억개 입니다. 입력층 하나와, 히든레이어 딱 하나로 구성된 DNN에서 필요한 weights의 수가 41억개라는 것은 말도 안되는 것 입니다. 이를 해결하는 것이 CNN 입니다. CNN은 필터라는 제한된 크기의 weights를 설정하고, 각 weights를 공유합니다. CNN은 Convolution 및 Pooling 연산을 반복적으로 수행하여 이미지 좌우 크기의 차원을 축소하고, 3차원 volume을 넓혀가면서 이미지에서 중요한 특징을 추출합니다. 이를 통해 DNN 보다 획기적으로 weights 를 줄입니다.
이후 등장하는 VGG, ResNet, GoogleNet, Inception-v1(v2, v3), R-CNN(Region CNN), YOLO(You Only Look Once) 망은 전부 CNN을 기반으로 하되, 그 층의 구조와 convolution 의 구성을 조금씩 수정한 모형들 입니다. 제 2편에서는 해당 내용을 살펴 볼 예정입니다.
(2) 자연어 처리
자연어와 같이 연속성 있는 데이터를 Sequence Data 라고 합니다. 자연어가 왜 연속성을 갖고 있는지는 몇 가지 단어를 통해 금방 알 수 있습니다. "안녕하세요" 에서 안 > 녕 > 하 > 세 > 요 가 순서대로 나타납니다. 그 누구도 "하세요녕안" 이라고 말하진 않습니다. 즉 "안"을 시작한 시점을 라고 하면, 에서는 "녕", : "하" … : "요"가 등장합니다. 예를 하나 더 들어보겠습니다.
"시간아 10 9 8 달려봐 10 9 8 7 6 내게로 5 4 3 빠져봐 5 4 3 2 1 Touchdown" 이라는 문장이 있습니다.
(트와이스-Touchdown 노래인데 출근길에 들으면 회사로 달려오고 싶은 노래입니다. 퇴근할때는 더욱 좋습니다.)
이 노래는 총 3분 22초의 길이를 가지고 있습니다. 그리고 위의 구절은 정확하게 0:00 ~ 0:09 까지의 구간입니다. 라고 하면, , , … , , , 이라는 순서 대로 나옵니다. 자연어는 정확하게 Sequence Data 입니다. 이러한 Sequence Data에 매우 적합한 딥러닝 모형이 하나 있습니다. 바로 RNN(Recurrent Neural Networks) 입니다. RNN 역시 제 3편 및 제 4편에서 설명드릴 예정이지만, 간략하게 말씀드리면 위와 같이 연속성 있는 데이터들을 계속 입력 받아 그 다음 문장(단어)을 출력하는 모형입니다. 즉, "시" 가 입력 데이터라면 그 다음 예상되는 출력값은 "간" 입니다. 그리고, 그 다음 "시간"이 입력되면 그 다음 출력값은 "아" 입니다. 마지막으로, "시간아" 가 입력되면 그 다음 예상되는 출력값은 "10" 입니다. 이런식으로 계속 순차적으로 다음값을 학습합니다. 그러면, 결국에는 사용자가 "시간" 이라는 입력값을 주면 RNN 모형은 "아"를 답하여 "시간아" 라고 말하는 것입니다. 하지만, RNN의 단점은 연속성 있는 데이터가 꾸준히 입력되면, 최신에 입력받은 데이터에 대한 가중치가 더 많이 부여되고 과거에 학습했던 내용은 그 가중치를 점차 잃어버린 다는 것 입니다. 즉, 마지막에 보았던 "5 4 3 2 1 Touchdown" 에 더 큰 가중치가 부여되어 있지,그 앞에 등장한 "5 4 3 빠져봐"는 이미 잊어버렸을 수도 있다는 것 입니다. 따라서, 이러한 단점을 보완하게 위한 LSTM(Long Short-Term Memory) 모형이 있습니다.
LSTM, Seq2Seq, Attention, BERT는 추후 제4편에서 더 설명하겠습니다. 참고로 말씀드리면 Seq2Seq는 Machine Translation(기계번역)또는 QA(Question and Answer)에 활용됩니다.
(3) 이미지 합성, 이미지 생성
딥러닝을 설명하는 여러가지 글 중에서, 고흐 "별이 빛나는 밤" 등 명화와 일반 사진을 합성한 사진을 보셨을 겁니다. 이처럼 Texture가 되는 이미지를 학습하고(명화) 여기에 새로운 사진을 입력하여, 두 개의 이미지 패턴이 서로 합성된 새로운 이미지를 만들어냅니다. 이러한 딥러닝 모형을 Neural Styler Transfer 이라고 합니다. 또한, 데이터를 생성하는 딥러닝 모형이 있습니다. 연예인 이미지를 학습하고 학습한 연예인 사진과 최대한 유사해 보이는 얼굴을 만들어 냅니다. 이걸 가능하게 해주는 모형이 GAN(Generative Adversarial Networks)입니다. 간략하게 설명드리면, 생성자(Generator)와 판별자(Discriminator)가 서로 경쟁하여 생성자는 자신이 입력받은 데이터와 최대한 유사한 분포를 가진 데이터를 생성하려고 하고, 판별자는 생성자가 만든 데이터가 진짜인지 가짜인지 판별합니다. 위의 두 가지 네트워크가 서로 경쟁하여 학습합니다. GAN이 주로 활용되는 사례는 AI 스피커에서 사용자의 음성이 실제로 사용자의 음성인지 아닌지를 판별하는 서비스가 있습니다. DCGAN(Deep Convolutional GAN)은 GAN에 Convolution Layer을 결합하여 GAN을 매우 안정화 시킨 모형입니다.
(4) 자율 주행
카메라를 통해 입력된 이미지에서 자율주행에 필요한 정적인 환경정보를 수집하고, 구별합니다. 이때 CNN 기반의 딥러닝 모형이 활용됩니다. 정적인 정보들은 차선, 표지판, 교통신호, 운전가능도로 등이 해당됩니다. 또한, 동적인 정보도 수집합니다. 주변 보행자, 차량 등등 이죠. 이러한 것들을 검출하기 위해 매우 빠르고 정확한 CNN 모형이 필요합니다. 카메라 정보 뿐 아니라 레이더, LiDAR, 각종 센서들이 감각 기관의 역할을 수행합니다.
카메라를 포함한 각종 감각정보를 통해 무인 차량은 자신의 움직임을 결정해야 합니다. 이때는 주로 강화학습(Reinforcement Learning)을 활용 할 수 있습니다. 강화학습은 특정 상태(State)에서 정의된 차량(Agent)이 현재 환경을 인식하여 선택가능한 보상(Reward)을 최대화 하는 행동을 결정하는 것을 말합니다. 이는, 카메라 또는 센서로 인식된 환경 하에서 최적의 행동을 찾도록 합니다. 예를 들어, 막히는 도로를 피해야 하는 상황, 교차로로 뛰어는 보행자를 피하는 것, 차선 변경하는 차량이 있으면 속도를 줄이거나 멈추는 행동등.. 특정 상황에서 받은 보상을 학습합니다. 계속 운전을 시도하면서 보상을 받고, 이를 통해 스스로 운전하는 방법을 배웁니다.
1.5 소결 (제 1장을 마치며)
여기서 1장을 마치도록 하겠습니다. AI, Machine Learning, Representation Learning, Deep Learning의 범위와 정의에서부터 딥러닝 기술의 시작이라고 할 수 있는 인공신경망의 기본 구조와 다양한 딥러닝 사례까지 살펴보았습니다. 매우 짧아서 아쉽죠? 그렇다면 바로 2장으로 넘어가 주세요! 만약, "아 나는 여기까지만 보겠다." 하시는 분은 여기까지만 보셔도 무방합니다. 한 가지 포인트는 다시 말씀드리고 싶습니다. 딥러닝이 결코 AI는 아닙니다. 그럼에도 불구하고, 딥러닝이 가져다 주는 이점은 분명히 있습니다.
새로운 비즈니스가 창출되거나 기존 비스니스에서 더욱 정밀한 서비스가 가능합니다. 자연어를 처리하는 챗봇과 같은 시스템은 이미 많이 활성화 되었습니다. 더 이상 예전의 심심이를 생각하면 안됩니다. 고객의 사소하지만 잦은 질문을 챗봇이 쉽게 해결 해 줄 수 있습니다. 또한, 수요예측/추천 서비스 등 고객에게는 보이지 않지만 뒷단에서 가공되는 데이터들이 더욱 정확해 집니다. 이는 결품률/재고보유비 감소, 타겟 마케팅으로 인한 고객감동 증가, 구매율 증가 등 고객만족과 비용효율화에 기여합니다.
자~!!, 2장도 한번 읽어보고 싶지 않으신가요? 인공신경망에 대한 설명은 길지 몰라도 개발 코드는 한줄로 끝납니다. 하지만, 아직 그 한줄을 바로 공개하진 않습니다. 왜냐면, 다 읽어야 그 한줄이 가진 진정한 의미를 알 수 있거든요. 여기서 1장을 마치겠습니다.
2. 인공신경망 깊게 이해하기
1장에서 우리는 딥러닝의 정의를 내리기 위해, 딥러닝이 포함된 집합을 알아보았습니다. 딥러닝에 대한 정의를 내리고, 가장 대표적인 기술인 인공신경망에 대한 용어를 살펴 보았습니다. 또한, 딥러닝 기술을 활용한 서비스와 이에 사용하는 알고리즘을 알아보았습니다. 2장부터는 본격적인 기술 내용을 다루고자 합니다. 여기부터는 수학기호가 여기 저기서 튀어 나올 수 있습니다. 하지만, 기호를 100% 이해하지 않으셔도 됩니다. 우리가 중요하게 살펴 볼 것은, 해당 기호들이 갖는 수학적 의미입니다. 이를 설명하는데 많은 지면을 할애 하겠으며, 독자 분께서는 기호가 아닌 수식의 의미를 살펴 보시기 바랍니다.
우리는 1.3에서 인공신경망의 용어를 정리하며 DNN이 무엇인지 알았습니다. 본 편에서는 DNN이 하나의 숲이라면, 그 숲을 구성하고 있는 나무(뉴런)에서 시작하여 우리의 시야를 점점 확대하고자 합니다.
2.1 단일 퍼셉트론에서 일어나는 일

[그림 9]은 단일 퍼셉트론(한개의 뉴런)에서 일어나는 모습입니다. (퍼셉트론은 뉴런 또는 Unit이라고 불립니다.) 해당 뉴런은 input layer의 바로 다음 hidden layer의 첫 번째 unit이 되겠죠? 해당 용어가 아리송하신 분들은 1.3절 인공신경망의 용어를 다시 한번 읽어 보시길 권장합니다.
[그림 9]의 퍼셉트론은 3개의 데이터를 입력받습니다. 입력된 3개 데이터는 퍼셉트론과 연결된 가중치와 곱해집니다. 여기에서 가중치(weight)의 개념이 등장했는데요. 이부분은 매우 중요합니다. 일단은 지금은 단일 퍼셉트론 전체를 한번 살펴보고, 가중치 역할에 대해 말씀드리겠습니다.
[그림 9]에서 가 입력되고, 각 입력된 정보는 각각 연결된 가중치()와 곱해져 퍼셉트론으로 입력됩니다. 그러면, 퍼셉트론은 각각의 곱을 다 더한 정보()를 만들어 냅니다. 뉴런은 만들어낸 정보를 활성화 함수(Activation Function)에 입력하여 이라는 결과를 만들고, 해당 정보를 다음 뉴런에게 전달합니다.
이 계산되는 과정에서 각각의 가중치의 합과 bias()가 더해지는 것을 알 수 있습니다. 바이어스(bias)는 사용자가 부여하거나 랜덤으로 초기화 되는 수 입니다. 바이어스는 입력된 신경망과 가중치 곱의 합이 가져야 할 최소 기준을 정의합니다. 인간의 임계점과는 조금 다른 개념입니다. 인간의 경우 임계점을 넘는 것은 전부 activate 되었지만, 인공신경망에서는 일단 다 전달하고 난 후, activation function을 통해 activate 여부를 결정합니다. 본 내용은 후술되어 있습니다.
(1) Bias 의 역할
만약, 이 1 이상일 때 뉴런이 활성화 된다고 가정하겠습니다. (activation function은 고려하지 않습니다) 그러면, 이어야 하겠지요. 해당 식에서 bias를 우변으로 넘겨보면, 가 됩니다. 만약, bias가 1로 설정되었다면 이 되므로, 입력값과 신경망 연결강도(weight) 곱의 합이 최소한 양수는 되어야 해당 뉴런이 활성화 됩니다. 입력된 정보 곱하기 연결된 신경의 강도 합이 무조건 0은 넘어야 한다는 것 이지요. 바이어스를 높게 설정하면 왠만한 뉴런들이 활성화 되지 않습니다. 이 말은 연결강도가 강력한 신호만 살아 남기겠다는 것 입니다. 우리 감각기관으로 따지면 특정 감각이 좀 둔감하다~ 정도 되겠죠. 반대로, 바이어스가 매우 낮다면 모든 신호들이 다 살아 남아져 흘러갑니다. 아까도 말씀드렸지만, 이것도 영 좋은 것은 아닙니다. (지금 언급한 문제는 Machine Learning의 Underfitting/Overfitting 문제입니다. 해당 부분은 추후에 다시 설명 드리겠습니다)
따라서 적절한 바이어스를 선택하는 것은 매우 중요한 문제입니다. DNN 초기에는 해당 값을 사람이 직접 초기화 시켜줬지만, 요즘에는 알고리즘이 알아서 초기화 하고 학습하여 계속 개선 해나갑니다.
(2) 활성화 함수(Activation Function)
에서 나온 결과인 은 units안에 있는 activation function의 입력값이 됩니다. 전달받은 모든 신호들의 합(바이어스 포함)을 activation function에 입력하여, 뉴런의 활성화 여부를 결정합니다. 인간의 신경망에서는 임계값을 넘은 것만 신호로 전달한다고 하였는데요, 인공신경망에서는 전달받은 모든 신호에 대해 activation function에 입력하고, 해당 함수를 통해 activate 여부를 결정합니다.
이것에 대한 논의를 좀더 하겠습니다. 예를 들어, 라는 activation 함수가 있고, 가 10 이상인 것만 activate 하겠다고 합니다. 그러면, 바이어스를 포함한 입력값()이 15를 넘어가면 해당 activation function은 다음 뉴런으로 신호를 전달 할 것입니다. 그럼 도대체 activation function과 bias의 차이는 무엇일까요?
결론부터 말씀드리면, bias는 activation function의 절편과 같은 역할을 합니다. 만약, 위의 사례에서 bias를 +5로 설정한다고 가정하겠습니다. 그러면, activation을 시킬 수 있는 신경합 최소값이 기존 15에서 10으로 줄어든 것 입니다. 수학적으로 살펴보겠습니다.
, and 이고, 는 activation function 입력값 이므로, 입니다. 에 대입하면, 이므로, 일 때 activate 됩니다.
하지만, bias가 인간 신경망의 "임계점"은 아닙니다. 인공신경망은 인간의 신경망과 다르게 bias가 어떤 값이라 하더라도 일단은 activation function으로 값을 전달하고, activation function의 기준에 따라 activate 합니다. 인공신경망은 인간과 다르게 특정 임계점을 설정 할 수 없으니, 우선은 bias를 포함한 값을 다 계산하고 activate 여부는 함수를 통해 공통된 기준을 가지고 일괄적으로 적용하겠다는 것 입니다.
그렇다면, 어떤 것이 activation function 이어야 할까요? 글 읽기를 멈추고 잠깐 생각해보시길 바랍니다.
아마도 activation function은 사람 뉴런의 역할을 해야 할 것입니다. 또한, "뉴런의 활성화"라는 것은 상황에 따라 달라지는 것이 아니라 일관성 있는 기준이어야 합니다. 더 나아가, 우리는 weights를 학습 해야 하는데, 이 학습을 "잘 할 수 있는" activation function 이어야 하겠지요. (아직 우리는 weights를 학습한다는 것은 배우지 않은 상태입니다)
생각을 좁혀봅니다. activation function에 무엇이 입력되나요? 입력받은 수() 곱하기 가중치()의 합입니다. 입력받은 수에는 학습하고자 하는 데이터가 포함됩니다. 우리의 학습데이터는 주어지는 것으로, 그 어떠한 수라면 상관 없습니다. 그러면, activation function이 입력받을 수 있는 수는 ~ 까지 모든 수가 될 것 입니다. 그리고 activation function은 무엇을 반환해야 하나요? activate 여부입니다. 즉, 어떠한 기준이 있어서 입력받은 값이 해당 기준을 넘어가는 순간 activate 되어야 하겠지요. 그럼 activate 되면 1 의 수가 나오고, activate 되지 않는다면 0 이라고 해볼까요?
그러면 우리의 activate function의 정의역은 에서 까지 이며, 치역은 1 또는 0 이 될 것입니다. 그럼, 이걸 가능하게 해주는 함수는 어떤 함수일까요?
(3) 다양한 Activation functions
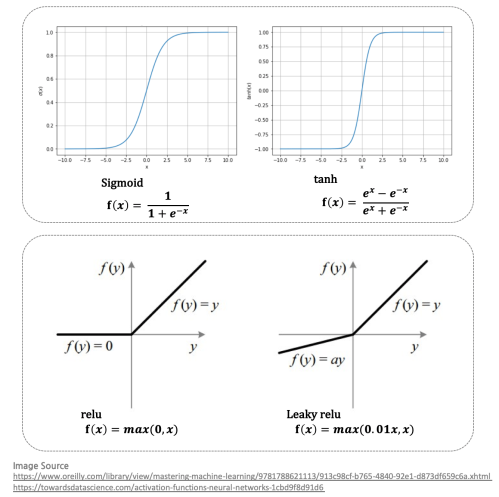
[그림 10]은 인공신경망에서 주로 사용하는 activation function들 입니다. 이들은 어떤 공통점이 있나요? 값에 따라 (또는 ) 가 특정 구간으로 한정됩니다.
[그림 10]의 좌상단 Sigmoid 함수의 경우 입력받는 의 값이 10에 가까울 수록(또는 까지) 가 1로 수렴합니다. 반대로, -10에 가까울 수록() 가 0으로 수렴합니다. 즉, 양의 큰 수가 계산되면 activate 됩니다. [그림 10]의 우상단 Hyperbolic tangent function(tanh)의 경우 sigmoid와 매우 유사한 커브를 보입니다. tanh function의 경우 sigmoid 함수의 크기와 위치를 조절한 함수입니다. 또한, Sigmoid의 경우 값이 0.5를 기준으로 1과 0으로 한정되었는데 tanh의 경우에는 0을 기준으로 1과 -1로 한정됩니다. tanh의 경우 학습 수렴 속도가 Sigmoid 보다 빠르고, 더욱 안정적입니다. 그 이유는 tanh 함수의 가운데 부분을 Sigmoid와 비교 해보시기 바랍니다. tanh의 가운데 부분 기울기가 Sigmod에 비해 더 가파르기 때문에, 추후에 배울 역전파(Backpropagation) 과정에서 미분값이 더 잘 계산됩니다. Sigmoid 함수의 경우, 딥러닝 모형이 최종적으로 출력해야 하는 결과가 1 or 0 과 같이 Binary Classification 인 경우 출력층 레이어의 Unit으로 활용합니다.
[그림 10]의 좌하단 relu 함수의 경우 일단 양수가 나오면 activate 됩니다. 음수가 나오면 0이 계산되어 activate 되지 않습니다. 우하단 Leaky relu의 경우 relu 함수보다 조금 더 변형된 것으로, 이 함수는 입력받은 신호에 대해 activate 여부를 binary 하게 결정하진 않습니다. 음수가 나오면, 해당 음수에 0.01 이라는 작은 수를 곱하여, 신호 자체를 작게 만들어줍니다. Relu와 Leaky relu의 경우 딥러닝에서 가장 많이 활용되는 activation function 입니다.
(4) Weights 의 역할
퍼셉트론에서 weights는 무슨 역할을 수행할까요?
결론부터 말씀드리면, 인공신경망에서 가중치의 역할은 앞에서 전달받은 정보를 얼마나 중점적으로 고려할 것인지 결정합니다. 잠시 논의를 인간의 신경망으로 전환해보겠습니다. 여러분 신경망의 특정 감각기관에서 반응하는 정도를 여러분이 직접 결정할 수 있나요? 식초를 한컵 마셔보신다고 생각해보세요. 이때 여러분들이 마음 속으로 "아 달다~" 라고 하면 식초에서 사탕맛이 나나요? 인간의 신경망이 반응하는 정도는 탄생에서 지금까지 꾸준히 학습되어온 과정입니다.
그렇다면, 인공신경망에서 꾸준히 학습하며 배우는 과정이 어느 부분일까요. 하나씩 살펴보며 무엇이 "배움"의 대상이 되는지 살펴보겠습니다.
첫째, input layer을 한변 살펴보겠습니다. input layer은 데이터를 입력받습니다. 데이터는 저희에게 주어집니다. 데이터는 신경망이 학습을 위해 사용하는 대상입니다. 사람의 학습으로 따지면 사과, 딸기, 전화기, 모자 등 어떠한 형태로서 존재하는 모든 객체들이겠죠. 알고리즘이 주도적으로 학습하여 변경시킬 수 없는 부분입니다.
둘째, layer안에 속해 있는 units 입니다. units에서는 입력받은 데이터()와 가중치()의 곱()을 더합니다. 그리고 다 더한 값을 자기 자신이 가지고 있는 activation function에 입력하는 역할을 수행합니다. 곱해진 값들을 다 더하는 역할만 수행합니다. 본인이 가지고 있는 activation function은 학습의 대상이 아닙니다. 자신으로 전달된 모든 정보를 다 더하고, 그 값을 전달하기만 할 뿐이죠.
셋째, 이전 layer의 unit과 와 다음 layer의 unit을 연결하고 있는 가중치는 어떨까요? 가중치는 앞에서 전달받은 내용을 자신과 연결된 뉴런으로 전달해줍니다. 앞에서 전달받은 내용에 대해 자기가 가지고 있는 weights를 곱합니다. 만약? weight 가 더 많이 곱해진다면요?
예를 들어보겠습니다. 입력받은 데이터는 1, 2, 3 으로 주어져 있습니다. 그런데, 여기에 각각 0.9, 0.5, 0.1이 곱해지면 어떻게 되나요? 입력*가중치 신호가 0.9( = 1 * 0.9), 1 (= 2 * 0.5), 0.3 (= 3 * 0.1)으로 변합니다. 입력된 데이터만 따지면, 3과 2에 가장 크게 반응해야 하는데, 오히려 2와 1에 더 많은 반응을 보이네요. 엇? 그렇다면 weights 의 크기에 따라 입력받은 정보 중에 어떠한 부분을 중점적으로 살펴봐야 할 지 알겠네요?
인공신경망에서 학습이 일어나는 부분은 바로 weights 입니다.
인공신경망은 가중치 크기에 따라, 뉴런과 뉴런 사이의 연결강도를 결정합니다. 그리고, 데이터를 통해 강력하게 연결될 부분의 가중치는 더욱 크게, 그렇지 않은 가중치는 작게 조정합니다. 논의를 잠시 1장의 Machine Learning과 Representation Learning으로 전환하겠습니다.
(5) Weights와 Representation Learning & Machine Learning의 관계
머신러닝은 과업(T)을 수행함에 있어 경험(E)를 학습한다고 하였습니다. 앞에서 언급한 대로, Deep Learning이 학습하는 것은 본인이 가지고 있는 weights 입니다. 그런데, weights가 학습하는 과정에서 어떠한 입력정보에 대해 더욱 많은 가중치를 부여하고 있다면 어떻게 되나요? 만약, 사과와 딸기를 분류하는 인공신경망이 사과와 딸기 꼭지 부분에 더 큰 가중치를 부여하고 있다면요? 또는, 아기가 "사과와 딸기가 다른 것이 뭐야?" 라는 물음에, 그림 낱말 카드에서 사과와 딸기 꼭지를 가르키며 "이 부분이 달라요" 라고 말하고 있다면요?
이러한 행동의 기저에는 사과와 딸기 꼭지 부분이 두 객체를 분류하는 Task에서 중요한 Feature로서 자리 매김 한 것 입니다. 학습 데이터 중에서 대표되는 부분을 중점적으로 학습한다는 개념. Representation learning 이었습니다.
인공신경망은 주어진 데이터를 통해, 자신이 가지고 있는 weights를 변경하면서 자신이 주어진 데이터 어느 부분에 더 중점적으로 반응할 지 결정합니다. 그리고 그 weights를 변경하는 과정을 우리는 "학습한다(training)" 라고 말합니다.
그렇다면, 간단한 샘플 예제를 통해 인공신경망이 어떻게 weights를 학습해 나가는지 알아보도록 하겠습니다.
2.2 단일 퍼셉트론을 활용한 부도여부 예측
| 부채 대 자산비율 () | 수입 대 지출비율 () | 신용등급() | 부도여부() |
|---|---|---|---|
| 1.5 | 0.5 | 5 | 1 |
| 1.5 | 2 | 4 | 0 |
| 0.5 | 0.2 | 7 | 1 |
| 1.5 | 1.5 | 3 | 1 |
| 0.1 | 1.3 | 1 | 0 |
[표 2]와 같은 5개의 훈련 데이터가 주어져 있다고 가정합니다.
인공신경망의 훈련과정은 크게 4단계로 이뤄집니다.
첫째, 전방전파(Feedforward) 둘째, 오차계산(Calculate Loss) 셋째, 역전파(Backpropagation) 넷째, 가중치 업데이트(Weight update)
우리는 [그림 9]와 동일한 퍼셉트론을 활용할 것입니다. 가중치와 바이어스는 각각 0.5로 초기화 되었으며, 해당 뉴런에서의 activation function은 sigmoid function 을 활용합니다.
(1) 전방전파(Feedforward) 과정
첫 번째 훈련 데이터가 다음과 같이 주어져 있습니다. 이며, 이때 부도여부는() 입니다. 또한 이와 연결된 weight와 bias가 각각 0.5로 초기화 되었습니다. 전방전파는 입력데이터와 가중치를 곱하고, bias를 더하는 과정입니다.
이므로,
값을 sigmoid 함수에 입력하면,
따라서, 입니다.
(2) 오차 계산(Calculate Loss)
부도여부, 질병여부, 스팸여부, 사과인지 딸기인지 여부 등 1 또는 0 으로 분류하는 모든 Task를 Binary Classification이라고 합니다. Binary Classification 문제에서 Loss Function(손실함수)은 Cross-Entropy를 활용합니다. 크로스 엔트로피는 정보이론(Information Theory)의 개념에서 나왔는데요, 간략하게 말씀드리면 인공신경망이 추정한 데이터의 분포와 학습하고 있는 실제 데이터의 분포의 차이를 최소화 하는 것 입니다. Cross Entropy 함수의 수식은 다음과 같습니다.
Cross-Entropy =
에 앞에서 나온 값을 입력하면, = = 입니다.
잠시 여기서 Cross Entropy의 특징을 한번 살펴보겠습니다.

인 경우부터 보겠습니다. Cross Entropy 값은 값이 됩니다. (Cross Entropy의 뒷 부분은 이 되기 때문에 사라집니다.) 이때 값이 작다면 어떻게 될까요? [그림 11]에서 볼 수 있듯, 함수 특성상 값이 1이하가 입력될 경우 음수가 출력되며, 입력되는 값이 0에 가까울 수록 그 값이 급격하게 커집니다.
이러한 수치연산이 갖는 의미는 무엇일까요?
모델이 학습한 결과가 1에 가깝다면 오차는 작게 나올 것 입니다. 하지만, 0에 아까운 숫자가 나오면 오차가 급격히 커집니다. 정답지는 1을 말하는데, 입력값이 0에 가깝다는 것은 두 결과가 전혀 반대라는 것 입니다. 즉, 정답과 학습한 값의 차이가 크면 클 수록 오차는 커지게 됩니다.
반대로, 인 경우는 어떨까요? Cross Entropy 함수 앞 부분은 사라지고, 뒷 부분만 남습니다. 만 살아 남습니다. 이때 이므로, 입니다. 결과값 a에서 1을 제외한 수를 입력하고 있습니다.
만약, 아까와 같이 값을 대입해보면 1 – 0.982 = 0.018 이 출력되며, 손실은 가 나옵니다. 즉, 해당 학습터의 정답은 부도가 아니라고 말하는데() 신경망에서의 결과는 부도에 가깝다는 결과()가 나왔기 때문입니다.
이처럼 손실함수로서 Cross Entropy가 하는 역할은, 주어진 데이터셋의 정답지에 따라 ( or ) 인공신경망이 만들어 낸 결과와 정답이 유사한 것은 오차가 작도록. 그렇지 않은 것은 오차를 매우 크게 계산합니다. 그렇다면, 모델은 어떻게 해야 오차를 작게 만들어 낼 수 있을까요?
(3) 역전파(Backpropagation) 또는 오차역전파
원래 역전파는 단일 퍼셉트론에서 나온 개념이 아닙니다. 로젠블라트가 제안한 단일 퍼셉트론으론 한계가 있었으며, 연구자들은 한계를 극복하기 위해 퍼셉트론 여러개를 쌓기 시작했습니다. 퍼셉트론이 많아지면서 각 퍼셉트론과 연결되어 있는 가중치를 어떻게 하면 학습을 통해 개선할 수 있을까 고민했습니다. 그 결과 나온 것이 역전파 입니다. 따라서, 역전파는 단일 퍼셉트론에는 맞지 않고, 다중 퍼셉트론에 적용되는 개념임을 미리 밝힙니다. 하지만, 저희는 역전파 과정이 무엇인지 이해해기 위해 샘플로 1개 퍼셉트론에 대한 역전파 과정을 알아보겠습니다.
역전파는 발생한 오차만큼의 정보량을 뒤로 보내, 신경망이 가지고 있는 weights를 업데이트 하는 과정입니다.
역전파를 위해 우리는 미분(differentiation)의 개념을 알아야 합니다. 미분이란, 함수의 변수가 매우 작은 수준으로 변화할 때 이에 대응하는 의 변화량을 말합니다. 다시 말하면, 값이 만큼 변화할 때 이에 대응되는 함수 의 변화량을 말합니다. 이때 이라 표현하면(0에 가까운 수 이지만 절대 0은 아닙니다.) 는 매우매우매우 작은 수가 되겠지요.
이것을 역전파에 쓰는 이유는, Loss 함수인 크로스 엔트로피는 2개 매개변수로 이뤄져 있습니다. 와 입니다. 여기에서 는 이미 고정되어 있는 데이터 이므로, 변화하는 값은 이 되겠습니다. 즉, Loss값을 결정하는 매개변수인 의 변화량에 따라 오차가 얼마나 변하는지 여부를 다시 앞으로 전파하여, 해당 오차만큼의 정보량에 대해 을 결정하게 한 weight에게 알려주겠다는 것 입니다. (니가 싼 똥 니가 치워라?)
다시 한번 정리하겠습니다.
을 결정하는 변수들은 무엇이었나요? 는 아니었습니다. 와 는 이미 학습 데이터에서 주어져 있는 값 입니다. 또한, activation function은 아무 죄 없는 함수 일 뿐 입니다. 결국 의 크기를 결정하는 변수는 weights()들 뿐 입니다. 또한 bias도 있었습니다. weights와 bias가 의 크기를 결정합니다. 손실함수 입장에서는 자꾸 정답지와 틀린 입력값이 들어오면 이렇게 생각 할 것입니다. "이봐 가중치! 너희가 만들어 내는 이 자꾸 안맞아. 너희들 변화에 따른 오차 변화분을 알려줄테니, 너희는 해당 정보를 토대로 값을 업데이트 해서 오차를 좀 작게 만들어봐." 라는 개념이죠.

[그림 12]는 오차역전파 과정을 그림으로 나타낸 것 입니다.
- 미분 설명
우선, [그림 12]에 나타난 새로운 기호들에 대해 설명드리겠습니다. 이라는 기호는 미분 기호를 나타냅니다. 자세하게는 편미분 기호라 하고, "Round" 라 읽습니다. 은 "라운드 분의 라운드 " 이라고 읽으며 이것이 의미하는 바는 함수 의 매개변수인 이 변화할 때의 함수 의 변화량 입니다. 또 다른 미분 기호로는 가 있습니다. 이것은 그냥 "디"(?)라고 읽습니다. 이 "디"는 함수의 모든 매개변수를 한번에 미분하라는 것 입니다. 이것을 전미분(total derivative) 이라 합니다. 이와 달리, 앞에서 나온 은 미분을 수행하는 함수의 매개변수가 2개 이상일 때, 모든 변수들의 변화는 고정한 채, 매개변수 중 특정 하나의 변화만을 살펴본다는 개념입니다. 이것을 편미분(partial derivative) 이라고 합니다. 이 편미분을 이라고도 간결하게 표현합니다. 이는 다변수 함수인 에서 매개변수 로 함수 를 편미분 한 것을 말합니다. 딥러닝에서는 편미분을 주로 활용합니다.
전방전파 : , 역전파 :
전방전파 : , ( = Sigmoid Function 기호표현), 역전파 :
전방전파 : , 역전파 : , , ,
역전파 결과는 해당 함수를 각 매개변수로 편미분 한 결과입니다.
- 합성함수의 미분 (Chain-Rule)
합성함수는 또는 라고도 표현하며, 함수 속에 함수가 존재하는 경우를 말합니다. 이것이 갖는 의미는 함수 의 결과값이 다시 함수 로 입력되는 것을 말합니다. 이러한 합성함수에서 매개변수 로 미분하게 되면 가 되는데요. 조금 헷갈릴 수 있으니 표기법을 바꿔 다르게 계산해보겠습니다.
라고 정의하고, 라고 재정의 하겠습니다. 입니다. 합성함수의 매개변수인 에 대해 편미분 할 경우 라고 쓸 수 있습니다. 이는 라이프니츠식 표기법 입니다.
이 기호가 중요하지 않습니다. Chain-Rule이 갖는 의미가 중요합니다.
어떤 함수의 매개변수인 이 있습니다. 이 친구는 자신이 변화할 때, 자기의 변화가 전체에 어떤 영향을 미치는 지 알고 싶습니다. 예를 들어보겠습니다. B회사 K사업부 A팀의 대리가 지금보다 업무량을 늘리는 경우 회사 매출에 어떠한 영향을 미치는 지 알고 싶다고 가정합니다. 이를 함수로 나타내면
=
이라고 표현됩니다. 매개변수 의 경로에 있는 모든 함수들의 편미분으로 표현할 수 있다는 것 입니다. (각각의 분모 분자가 서로 삭제되는 것은 아닙니다.)
- 역전파 과정에 Chain-Rule 적용
그럼 이를 역전파 과정에 적용하도록 하겠습니다. 우리의 목표는 각각 weights의 변화에 따른 손실함수의 변화를 파악하여, 이를 다시 되돌려 주는 것 입니다.
즉, , , , 를 알고 싶습니다.
이들이 Loss계산을 위해 이동하는 경로는 , 그 다음 이고, 마지막으로 입니다. 이를 연쇄법칙을 통해 역으로 나타내면,
=
=
=
=
각 항목에 대해 위에서 계산한
, , , , , 을 삽입하면,
다음과 같이 정리됩니다.
=
=
=
=
이것들을 계산하면 됩니다.
(4) 가중치 업데이트
역전파를 통해 자기자신의 변화가 오차에 얼마나 영향을 미치는지 계산 할 수 있었습니다. weights는 자기 자신을 그만큼 변화시켜야 한다는 것 입니다. weight & bias의 업데이트는 다음 식을 이용합니다.
여기에서 는 학습률(learning rate)라는 것으로, 사용자가 임의로 부여하는 수 입니다. 보통은 0.01 값을 부여합니다. 학습률이 커지면 오차도 그만큼 커지게 되고, 한번에 업데이트 해야 할 크기가 커지겠죠? 그런 경우 학습은 빨라 질 수 있으나, 최적해로의 수렴가능성이 떨어집니다. 반대로, 0.001과 같이 너무 작은 수로 설정하면 한번에 찔끔 찔끔 학습되니 학습속도가 매우 느려 질 것 입니다. 따라서, 적절한 학습률을 설정하는 것이 중요합니다. 일반적으로는 0.01 이지만, 0.1 또는 아예 1로 하는 경우도 있습니다. 여기에서 학습률은 0.01로 부여하겠습니다.
앞에서 계산된 을 대입하여 계산하면,
= = =
= = =
= =
= =
과 같습니다. 따라서, 첫 번째 학습 결과 weights 는 위와 같이 변합니다. 그후, 두번째, .. 마지막으로 다섯번째 학습데이터들을 다 넣어보며 위의 방법에 따라 weigths를 학습 해 나갑니다. 5개의 학습데이터에 대하여 한 번의 학습이 끝나면 weights는 다음과 같습니다. , , ,
자세한 풀이과정은 첨부된 엑셀 파일(chap1_example2.2.xlsx)을 통해 확인 해주세요. 여러분께서는 learning rate를 하나씩 바꿔가면서 실험 해보시기 바랍니다. leraning rate의 숫자가 커질수록 weights의 변화가 많이 발생함을 확인 할 수 있습니다.
- 훈련 파라메터 설명 (batch size, epoch)
딥러닝 학습시 사용자가 제공해야 할 파라메터가 다수 존재합니다. 위에서 살펴본 learning rate가 있고, 이 뿐 아니라 batch size, epoch도 대표적인 파라메터 입니다. 위의 2.2절 사례에서는 batch size = 1 , epoch = 1 입니다. 가중치 업데이트를 데이터 하나 마다 수행하기 때문입니다.
보통의 경우 학습에 활용하는 데이터는 매우 많습니다. 예를 들어, 사진 1,000,000장을 학습한다고 하면 [표 2]의 행 수가 1,000,000개로 구성 될 것 입니다. 이런 경우, 데이터 1개 학습마다 weights를 업데이트 하기에는 번거롭습니다. 따라서, batch size를 주어 한번에 뭉태기로 학습하고, 해당 오차의 평균값을 구해 weight를 한번에 업데이트 합니다. 보통 32, 64, 256, 512, 1024처럼 2의 거듭제곱꼴로 으로 batch size를 설정합니다. 이는 GPU 사용시 메모리 할당과 관련된 문제여서 2의 거듭제곱꼴로 부여하는 것이 좋다는 말이 있습니다.
또한, epoch는 해당 데이터를 몇 번 반복해서 학습할 것인가를 의미합니다. 시험기간에 책을 딱 한번만 볼 것이냐? 아니면 2번 3번을 반복해서 풀 것이냐를 의미합니다. 본 사례 문제에서 epoch가 1인 것은 5개 데이터를 딱 한번만 학습해서 weights를 구했기 때문입니다. 실제로는 1,000번 정도 학습을 반복합니다.
일례로 위의 1,000,000개 이미지를 학습하는 모델에서 배치사이즈가 1,024로 주어졌고 epoch가 20번으로 부여되었다면, 데이터 전체 대상 1회 학습시에는 977(976.6개의 배치 )번 반복을 수행하고 이를 다시 20번 수행하므로, 총 19,540번 반복하게 됩니다.
그렇다면 epoch가 높으면 높을수록 좋을까요? 절대 아닙니다. epoch를 크게 줄 수록 모델이 학습하는 데이터에만 중점적으로 학습됩니다. 이를 Overfitting Problem(과대적합) 이라고 합니다. 풀어야 할 문제가 수학, 국어, 사회, 영어가 있는데 수학만 냅다 공부해버린 격이 되는거죠. 따라서, 이를 해결하기 위해 모델 학습시 Early Stopping을 위한 Callback 함수를 선언합니다. 학습을 수행함에 있어 일정한 반복기간 동안 정확도(혹은 손실량)의 개선사항이 없는 경우 1,000번을 다 수행하지 않고 중간에 학습을 멈추게 합니다. 이 뿐 아니라, Drop-Out 등 여러가지 파라메터를 활용하여 모델의 Overfitting Problem을 해결해줘야 합니다. 이러한 부분은 추후 설명드리겠습니다.
2.3 단일 퍼셉트론의 한계
지금까지 한개 퍼셉트론으로 구성 된 인공신경망의 학습 과정을 살펴 보았습니다. 하지만, 왜 단일 퍼셉트론을 쓰지 않고, 신경망이 더 깊어지게 되었는지 이유를 설명드리겠습니다.
제가 여러분에게 직선 하나를 빌려드리겠습니다. 지금부터 여러분은 마음 속에 있는 직선 하나를 가지고 다음 [그림 13]의 점을 분류 해보시기 바랍니다. 직선 하나를 그어 파란색 점은 파란색끼리, 노란색은 노란색점 끼리 모여있으면 됩니다.

잠시 시간을 드리겠습니다.
좀 그려보셨나요? [그림 13]은 XOR(eXclusive OR) 문제로서 직선 하나로는 4개의 점을 색상별로 분류 할 수 없습니다. 이것이 단일 퍼셉트론이 쇠퇴기를 맞았던 이유이며, 단일 퍼셉트론이 아닌 다중 퍼셉트론을 활용하게 된 이유입니다. 물론, 단일 퍼셉트론이 Sigmoid 함수를 활용하여 직선이 아닌 약간 곡선 형태의 선을 그려내지만, Sigmoid의 선 하나로는 XOR을 분류 할 수 없습니다. 그러면 어떻게 해야 이 문제를 해결 할 수 있을까요?
바로 퍼셉트론을 여러개 만들어 선을 여러개 긋게 하는 것 입니다.
2.4 다중 퍼셉트론의 등장 (MLP)
1969년에 Marvin Minsky 교수가 "단일 퍼셉트론은 XOR 문제도 하나 해결하지 못하는 바보다!" 라고 말합니다. (물론 그냥 말하면 안되니까 "Perceptrons: an introduction to computational geometry" 이라는 책을 통해 말했답니다.) 이후 신경망은 쇠퇴기를 겪습니다. 하지만, 끝까지 포기하지 않은 이가 있으니.. 바로 "Geoffrey Hinton" 교수 입니다. 물론 (McClelland, James L., David E. Rumelhart 와 같이 연구합니다.)
힌튼 교수는 1986년 히든 레이어를 가진 퍼셉트론, MLP(Multi-Layer Perceptrons)와 MLP에서 W, b를 효과적으로 학습할 수 있는 역전파 알고리즘(Backpropagation)을 제안합니다. 드디어 다중 퍼셉트론이 등장합니다.

[그림 14]는 3개 층(Hidden Layer 2, Ouput Layer 1)을 갖는 MLP 모형입니다. 만약, "4개인데 왜 3개라고 해?"라는 궁금증이 생기신 분들은 1.3절을 빠르게 읽고 오시기 바랍니다.
- 다중 퍼셉트론에서 사용하는 수학기호 정리
드디어 다중 퍼셉트론이라는 숲으로 들어왔습니다. 실제로 서비스에 활용하는 네트워크는 [그림 14]에서 처럼 간단한 모형이 아닙니다. 또한, CNN부터는 네트워크가 상당히 깊은 모형을 만나게 됩니다. 깊은 네트워크를 간결하게 설명하기 위해 수학 기호를 사용해야 합니다. 여기에서는 해당 기호들에 대해 짚고 넘어가도록 하겠습니다.
네트워크&데이터 크기와 관련된 기호
: 데이터셋 개수 (2.2의 사례의 경우 )
: 한번에 입력되는 독립변수의 수, 혹은 차원의 수 (2.2의 사례의 경우 )
: 출력되는 종속변수의 수 (2.2의 경우 )
: 번째 레이어의 히든 유닛의 수 (2.2의 경우 이며, [그림 14]의 경우 , )
: 네트워크의 전체 레이어 수 ([그림 14]의 경우 )
각 객체들에 대한 정의
- : 학습데이터셋에 대한 표현 (2.2 데이터셋의 경우 이며, 이를 행렬로 표현시 다음과 같음)
- =
- : i 번째 학습데이터를 하나의 열벡터(Column Vector)로 표현
- : 학습데이터셋의 Label 값에 대한 표현 (2.2 데이터셋의 경우 )
- =
- : i번째 학습데이터를 표현 ()
- , ,
- = 과 같이 표현 됩니다.
- : 번째 레이어의 bias 벡터 [그림 14]에서는 bias를 표현하지 않았지만, 각 hidden layer의 유닛 수 만큼 bias가 열벡터로 존재합니다.
- =
- = 번째 레이어에 입력되는 입력값 () or ()
- = 번째 레이어 activation function 결과값 ( or
실제 계산식의 적용 (첫 번째 예제 데이터만 적용 , batch size = 1)
첫 번째 입력데이터 =가 Feedforward 되는 과정은 다음과 같습니다.
(1) = + = =
(2) = +=
=
(3) = + = =
이러한 과정을 통해 최종적으로는 스칼라 값을 갖는 이 출력되고, 이를 와 비교하여 Loss를 계산합니다.
역전파 과정은 생략하도록 하겠습니다. 2.2절에서 첨부한 엑셀 파일을 참조하시면 학습하는 데 많은 도움이 되실겁니다.
2.5 2장 소결
마지막으로 다중 퍼셉트론 구현을 위한 의사코드(Pseudo-Code)를 소개하며 2장을 마치도록 하겠습니다.
- DNN Pesudo-Code
| No | Process | Loop |
|---|---|---|
| 1 | 파라메터 초기화( and ) | |
| 2 | 전방전파 계산 – – | * |
| 3 | 손실계산 () | * |
| 4 | 역전파 계산 – , , | * |
| 5 | and 업데이트 수행 | * |
| 6 | 최종 예측수행 |
- 제 1편 딥러닝의 시작과 인공신경망을 마치며…
상세한 설명을 하다 보니 내용이 많이 길어졌습니다. 하지만, 제 1편에서 알아봤던 내용은 딥러닝의 기본 신경망 입니다. 또한, 딥러닝 학습과정인 전방전파-오차계산-역전파 과정은 CNN, RNN, LSTM, GAN 등 대부분 모형에 적용되는 일종의 규칙입니다. 따라서, 본 내용을 정확하게 이해하신다면 어떤 모형을 배운다 하더라도 금방 이해하실 수 있습니다. 이를 위해, 내용이 다소 길어지더라도 부연설명을 많이 하려고 했습니다. 읽어주셔서 정말 감사합니다. 다음 장에서는 간략한 구현 코드와 추후 다룰 내용을 말씀드리겠습니다.
3. 인공신경망 구현해보기
딥러닝 개발을 위한 언어는 주로 python을 활용합니다. 대용량 벡터&행렬 연산을 매우 빠르게 처리하는 좋은 라이브러리 들이 있기 때문입니다. 또한, python에서는 딥러닝 개발을 위한 매우 편리한 고성능 API를 제공하고 있습니다. (tensorflow/keras) 따라서, 여러분이 처음 딥러닝 개발을 하고자 한다면 python 환경에서 하시기를 추천합니다. 하지만, 필수는 아닙니다. tensorflow는 java, C, GO 등을 지원하고 있기 때문에 tensorflow.org 홈페이지에 직접 방문하셔서 본인이 주로 활용하는 언어의 API를 설치하셔서 사용하시면 됩니다.
만약, 딱히 없으시다면 python을 설치하세요. Win 환경에서는 python을 직접 설치하지 마시고, Anaconda를 설치할 것을 추천합니다. Linux/Mac 환경에서는 내장된 패키지 관리도구(apt-get, brew, …)를 통해 설치하시면 됩니다. Mac의 경우 2.7 / 3.x 버전이 기본으로 내장되어 있으니, 내장된 Python을 활용하셔도 됩니다. 파이썬은 2과 3버전대로 나뉘는데, 2 버전대(2.x.xx)는 2020년 부터 지원이 종료되므로 python 3.6 이상의 버전을 활용하시면 됩니다. 또한, 파이썬 설치시 너무 최신버전을 설치하시지 마시고 3.6.6 버전을 설치하세요. 또한, tensorflow도 1.13 버전을 설치하시길 권장합니다. Win의 경우 Anaconda 홈페이지 repository에서 버전을 고르시거나, 일단 최신버전으로 설치 후 Anaconda Navigator에서 python을 3.6.6으로 downgrade 하시면 됩니다.
python 기반 환경설정을 하는 부분에 있어서는 추후 번외편. 딥러닝 개발환경 구축하기에서 중점적으로 다뤄 볼 계획입니다. 혹시나 시도하시다가 잘 안되는 경우에는 댓글로 남겨주시면 해결을 도와드리겠습니다 !!
만약, 그 어떠한 것도 내 컴퓨터에 깔리는 것이 싫다고 하시는 분들은 구글의 Colab(클라우드 기반의 python Notebook Instance)을 실행하시고, 하단 코드를 바로 복붙하여 실행해보시기 바랍니다. Colab에 대한 상세한 설명은 번외편. 딥러닝 개발환경 구축하기에서 다루겠습니다.
일단, 본 3장에서는 python 코드를 통해 간단한 신경망을 알아보겠습니다.
x# python2 버전 충돌을 막기 위한 패키지 import from __future__ import print_function # keras 패키지 불러오기 import kerasfrom keras.datasets import mnist from keras.models import Sequentialfrom keras.layers import Dense, Dropoutfrom keras.optimizers import RMSprop# Model 훈련을 위한 파라메터 설정 batch_size = 128num_classes = 10 # 최종 예측해야 하는 결과값이 0~9까지 10개 입니다. epochs = 20# Keras를 통해 온라인으로 제공하는 mnist 데이터를 다운받을 수 있습니다.# Mnist 데이터는 0 ~ 9 까지의 손글씨 데이터를 의미합니다. (x_train, y_train), (x_test, y_test) = mnist.load_data()# 데이터의 차원이 m = 60000, n_x = 784의 매트릭스로 변환됩니다.# mnist 데이터는 28*28 이미지 데이터이므로, 28*28 = 784의 입력변수 갯수를 갖습니다. # 정리하면, 훈련데이터의 갯수가 60,000개 / x 독립변수가 784개라는 것 입니다.x_train = x_train.reshape(60000, 784)# 10,000개는 훈련에 참여시키지 않고 test 할때 활용하려고 남겨둡니다. x_test = x_test.reshape(10000, 784)# 데이터 타입을 32비트 부동소수형으로 바꿔줍니다. 부동소수형은 소수점을 지정하지 않은 숫자를 말합니다. x_train = x_train.astype('float32')x_test = x_test.astype('float32')# 칼라 이미지의 경우 R, G, B 채널이 존재하고, 각 픽셀값이 0~ 255까지 숫자로 표현됩니다. rgb(255,255,255)라고 사용하는 개념입니다. # Mnist 데이터의 경우 흑백 이미지로 단일 채널입니다. 만약 칼라였다면 3개 채널에 대하여 정규화를 해 줘야 했겠지만 흑백이기 때문에 단일 채널에 대해, 픽셀이 가질 수 있는 최대값으로 나눠 전체 데이터를 0~1 사이 값으로 정규화 합니다.x_train /= 255x_test /= 255print(x_train.shape[0], 'train samples')print(x_test.shape[0], 'test samples')# 우리가 맞춰야 하는 정답지는 0~9까지의 숫자 입니다. 해당 데이터를 one-hot vector로 바꿔줍니다.y_train = keras.utils.to_categorical(y_train, num_classes)y_test = keras.utils.to_categorical(y_test, num_classes)#### 여기부터가 DNN 모형 생성 부분입니다. #####Sequential()객체로 모델을 선언함으로써, 코드를 한줄 한줄 추가시켜 레이어를 층층히 쌓을 수 있도록 합니다. model = Sequential()# input_layer = (batch_size, 784) & hidden_layer_1 = (batch_size, 512)model.add(Dense(512, activation='relu', input_shape=(784,)))model.add(Dropout(0.2))# hidden_layer_2 = (batch_size, 512)model.add(Dense(512, activation='relu'))model.add(Dropout(0.2))# output_layer = (batch_size, 10)model.add(Dense(num_classes, activation='softmax'))# 3개 층으로 구성된 DNN 모델이 생성됩니다.# 모델 생성결과 None 이라고 표현되는 부분이 있는데, 그것은 batch_size를 의미합니다. batch_size는 사용자가 학습을 위해 부여하는 parameter이기 때문에, 모델에서는 해당 부분을 slack으로 남겨두게 됩니다. 따라서, None이 찍힙니다. model.summary()# 모델 컴파일 # categorical_crossentropy는 2개 이상의 다범주를 분류할 때 쓰는 loss 함수입니다. 최적화 기법으로는 RMSprop를 활용하는데, 이는 모델이 loss를 최소화 하는 W, b를 효과적으로 찾기 위해 선언하는 함수입니다. 최적화 문제 해결시 gradient를 계산하는데 gradient의 최신성에 더 큰 가중평균을 주는 개념입니다. # optimizer로 RMSprop와 Adam(만든사람 이름)을 주로 활용합니다. # 0~9를 맞춰야 하는 문제이기 때문에, 모델의 학습 평가를 위해 정확도(accuracy)를 측정합니다. model.compile(loss='categorical_crossentropy', optimizer=RMSprop(), metrics=['accuracy'])# 학습과정을 담을 변수(history)를 선언하고, 학습에 필요한 paramter을 입력하여 학습을 수행합니다. history = model.fit(x_train, y_train, #훈련데이터 X와 정답지 y를 학습하라는 것. batch_size=batch_size, #배치사이즈 (128) epochs=epochs, #몇번 반복해서 풀 것인가? (20) verbose=1, #훈련 log 출력정도 validation_data=(x_test, y_test)) #훈련에 참여하지 않는 데이터를 통해, 중간중간 모델학습이 얼마나 잘 되었는지 평가합니다. # 훈련에 전혀 참여하지 않았던 데이터를 예측하게 함으로써, 모델 예측력을 최종평가 해봅니다.# model.fit의 validation_data 변수에 들어가는 변수와 같아도 괜찮습니다. model.fit은 중간중간 확인해보는 개념이고, 마지막에 쓰이는 model.evaluate는 최종점검 개념입니다. score = model.evaluate(x_test, y_test, verbose=0)print('Test loss:', score[0])print('Test accuracy:', score[1])제 1편을 마치겠습니다. 잘못 설명된 부분 및 추가적으로 궁금하신 내용은 댓글 혹은 이메일(jeonjoohyoung@gmail.com)을 통해 언제든지 연락주세요! 읽어주셔서 감사합니다.
마지막 편집 일자 : 2019-05-26
tjddlfn
2021년 04월 22일 @ 10:04 오전
굉장히 유익하게 보았는데 다음글들은 아직 안올라온 것인가요?